حل معادله انتقال-پخش دو بعدی در حالت ناپایا با روش حجم محدود با فرترن

حل معادله انتقال-پخش دو بعدی در حالت ناپایا با روش حجم محدود با فرترن

در این پروژه که با فرترن انجام شده است معادله  2D Unsteady convection diffusion   با روش های حجم محدود اختلاف مرکزی و هیبریدی حل شده است.

در مثال مورد نظر ، آلودگی یک کارخانه وار محدوده ای از رودخانه شده است و در دو حالت زیر توزیع غلظت آلودگی  در زمان های مختلف بدست آمده است:

دریافت فایل

تحلیل ارتعاشی تیر به کمک روش کوادراتور دیفرانسیلی

محاسبه فرکانس طبیعی تیر اولر-برنولی و تیموشنکو با استفاده از روش DQ هدف پژوهش حاضر می‌باشد. بیشتر پژوهش‌های انجام شده بر روی تیر اولر-برنولی (تیرهای دراز و باریک) می‌باشد و اثر اینرسی دورانی و تغییر شکل برشی لحاظ نشده است. از آنجا که چنین اثری را در مورد تیرهای کوتاه نمی‌توان نادیده گرفت، بررسی آن در مورد تیرهای کوتاه ضروری به نظر می‌رسد.

در فصل دوم پژوهش‌های پیشین در زمینه DQ بررسی خواهند شد.در فصل سوم به روش DQ، معادلات تیر اولر ، تیموشنکو، چگونگی گسسته‌سازی معادلات حاکم با استفاده از DQ و روشهای مختلف اعمال شراط مرزی پرداخته می‌شود.در فصل چهارم نتایج و تاثیر تعداد نقاط دقت و روابط نقاط دقت خواهند شد. در فصل پنجم به نتایج حاصل از این پژوهش پرداخته شده است.

برنامه‌های کامپیوتری تعیین فرکانس طبیعی تیرها

برنامه شماره 1 ماتریس‌های ضرائب وزنی استفاده شده در روشهای اصلاح ماتریس ضرائب و جایگزینی مستقیم شرایط مرزی را محاسبه می‌کند. برنامه شماره 2 ماتریس‌های ضرائب وزنی در روش دلتا را محاسبه می‌کند. برنامه شماره 3 فرکانس‌های طبیعی تیر اولر برنولی را به روش اصلاح ماتریس ضرائب محاسبه می‌کند. برنامه شماره 4 فرکانس‌های طبیعی تیر اولر برنولی را به روش جایگزینی مستقیم شرایط مرزی محاسبه می‌کند. برنامه شماره 5 فرکانس‌های طبیعی تیر اولر برنولی را به روش دلتا محاسبه می‌کند. برنامه شماره 6 فرکانس‌های طبیعی تیر تیموشنکو برای تیر دو سر آزاد محاسبه می‌کند.

این پروژه با فرمت word و تعداد 60 صفحه می باشد ضمنا فایل ارائه پاورپوینت به تعداد 37 اسلاید نیز ضمیمه می باشد.

مقاله ترجمه شده ورد برق - مطالعه و بررسی روش نزولی برای کاهش ولتاژ مازاد ( صاعقه ) در ایستگاه فرعی نیرو 8 صفحه

چکیده  
در مقاله  کنونی  پدیده  انتشار  ولتاژ مازاد در  یک  ایستگاه  برقگیر  380 کیلو  واتی  شبیه  سازی شده  است . تاثیر  نضصب  مهار جریان نابهنجار  بر  نقطه  اوج  ولتاژ ایاد شده  ترسیم  و تشریح  شده  است  . ابزار کاهنده ولتاژ نوین  در قالب  یک  فیلتر  ولتاژ بالا  ارائه  شده  و فرآیند  بسط  و بررسی  آن  در امتداد  نتایج  متمایز  تشریح گردیده  است  . همان  گونه  که  نشان  داده  شده  است ، دستگاه  ارائه  شده  می تواند در  شبکه  های HV به  عنوان  جایگزین  و ارقتا دهنده  سطح  عملی  برای فرآیندهای کاهش  ولتاز اضافی  استعمال شود . تمام مطالب شبیه  سازی با استفاده  از پکیج  بر  مطلب  جمع  اوری  و گردآوری شده  است  

حل تمرین اول فصل پنجم کتاب دینامیک سیالات محاسباتی هافمن با فرترن 90

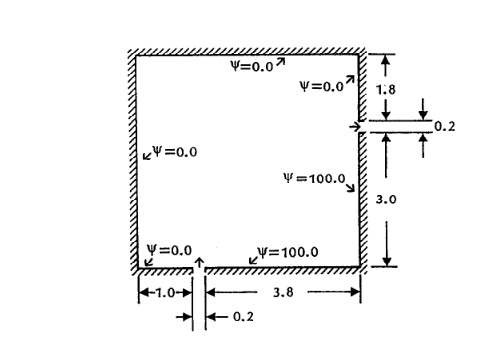
هندسه و شرایط مرزی  مسئله مورد نظر به صورت زیر است:

مسئله مورد نظر با کد  فرترن و با روش های زیر حل شده است:

PSOR

ADI

LSOR

گوس نقطه به نقطه

گوس خط به خط

 توضیح کامل روش و  نتایج توزیع جریان در فایل گزارش کار(word) آمده است

مقاله روش ژاکوبی برای حل مسائل غیر خطی

روش ژاکوبی در واقع تعمیمی از روش سیمپلکس برای حل مسائل خطی می‌باشد یا به عبارت دیگر روش ژاکوبی در حالتی خاص همان روش سیمپلکس می‌باشد

بخش دیگری از متن مقاله:

برای شناسایی نقاط بحرانی از شرایط کافی به شرح زیر استفاده می کنیم:

شرایط کافی برای نقطة بحرانی  جهت اکسترمم بودن آن است که ماتریس هسیان محاسبه شده در نقطه

هنگامی که  می نیمم است مثبت باشد .هنگامی که  ماکزیمم است منفی باشد .

برای روشن کردن این مفهوم تابع f(x1 , x2) را در نظر می گیریم. هدف می نیمم کردن تابع با توجه به محدودیت g1(x1 , x2) = x2 – b=0 می‎باشد. (b ثابت است.) منحنی ایجاد شده توسط سه نقطة C , B , A مقادیری از f را نمایش می‎دهد که محدودیت اعمال شده همواره برآورده می گردد. روش ژاکوبی، گرادیان f(x1 , x2) را در هر نقطه ای از منحنی ABC تعریف می‌کند. هر نقطه ای که مشتق آن برابر صفر گردد نشان دهنده یک نقطه بحرانی برای این مسئله مقید می‎باشد که در شکل زیر نقطة B ، نقطه موردنظر می‎باشد.

با استفاده از ق تیلور برای نقاط  در همسایگی قابل قبول x داریم:

هنگامی که  خواهیم داشت:

و از آنجا که g(x)=0 در نتیجه  بنابراین خواهیم داشت:

حال یک دستگاه با (n+1) مجهول و (m+1) معادله خواهیم داشت که مجهولاتمان درایه‌های  می باشند  با مشخص شدن  پیدا می‎شود. و این بدان معناست که در واقع m معادله با n مجهول داریم. اگر m>n آن گاه حداقل (m-n) معادله زائد می باشند. پس از حذف آنها، سیستم به تعداد کارایی از معادلات مستقل مانند  کاهش خواهد یافت. برای حالتی که m=n باشد جواب می‎باشد و این نشان دهنده آن است که X همسایگی قابل قبول ندارد و فضای حل تنها از یک نقطه تشکیل یافته است. در اینجا این حالت موردنظر نیست و ما به بررسی حالت m < n می‎پردازیم.